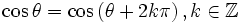Saiba por que a vida de Pitágoras, inventor de um famoso teorema, é um enigma!
No fim do recreio, a garotada entrou na sala desanimada. O professor havia escrito no quadro a lição do dia: teorema de Pitágoras. Notou a tristeza da turma e perguntou qual era o problema. "A matemática, professor!" -- respondeu um aluno -- "O senhor vai ensinar mais uma fórmula!"
-- Quem inventou isso? Para quê serve? -- indagou outro estudante. Era a chance que o mestre esperava para dar uma aula diferente. Antes de explicar o significado do teorema e sua aplicação, falou sobre quem o criou: Pitágoras, filósofo e matemático grego que viveu no século 6 antes de Cristo (a.C.).
A história de Pitágoras é cheia de mistérios! Há poucas imagens de seu rosto (veja ao lado um busto dele). Ninguém sabe ao certo como ele morreu e nem se histórias que contam sobre ele são verdadeiras. O matemático fundou uma associação religiosa e secreta, foi perseguido por suas idéias e odiava ser contestado. Percebeu a harmonia dos sons e criou o talvez mais famoso teorema da matemática, que tornou mais precisas as construções. Suas descobertas revolucionaram a matemática e o conhecimento humano.
Ele deve ter nascido por volta de 580 a.C., na ilha de Samos, hoje parte da Grécia. Adulto, foi ao Egito e à Babilônia. Mas não buscava diversão! Queria aprender matemática, pois egípcios e babilônios faziam cálculos complexos para construir prédios, por exemplo. Para eles, os cálculos deviam dar a resposta certa. Por que isso acontecia era irrelevante.
Esse modo de pensar incomodava Pitágoras. Ele queria entender os números e não apenas utilizá-los. Voltou à ilha de Samos para fundar uma escola de filosofia e matemática e buscar o significado dos números. Ao chegar, soube que o tirano Polícrates governava e a sociedade se tornara intolerante e conservadora.
Polícrates seguia o orfismo, doutrina segundo a qual o homem deveria idolatrar o deus Dionísio para ser liberto. Pitágoras a criticava, pois achava que o caminho para a salvação era a matemática. Quando o tirano o convidou para participar da corte, recusou a oferta. Sabia que ele queria silenciá-lo! Fugiu para uma caverna, onde estudava sem temer perseguições. Como queria transmitir conhecimentos... pagava um aluno! Criou a escola Semicírculo de Pitágoras e o estudante gostou tanto dele que passou a segui-lo sem ganhar dinheiro. Ao sentir que precisava ensinar mais pessoas, Pitágoras deixou sua terra natal com a mãe e o discípulo.
Em Crotona, cidade no sul da Itália, conheceu Milo -- um homem forte que gostava de matemática e filosofia e deu sua casa para Pitágoras fundar a Irmandade Pitagórica, associação religiosa e filosófica com cerca de 600 membros, os pitagóricos. Quem seriam eles?
A Irmandade Pitagórica
Conheça a filosofia e as principais atividades dessa sociedade secreta
Os pitagóricos trocavam conhecimentos sobre temas variados. Eram inteligentes, deviam entender ensinamentos e dar novas idéias. Doavam seus bens para a irmandade e não comiam carne. Juravam não revelar descobertas científicas da sociedade para o mundo. A pena para os desobedientes era a morte.
Acreditavam que as relações entre os números revelariam segredos do universo e colocariam o homem próximo dos deuses. Para eles, os números pares e ímpares eram opostos. Como a sua soma forma novos números, representa a perfeita conciliação de contrários. A realidade funcionaria da mesma forma. As coisas são criadas por idéias opostas e é da oposição que surge o equilíbrio e a harmonia do universo.
Pitágoras proibia seus pupilos de estudar ou divulgar números irracionais. Ele os odiava porque contradiziam a teoria dos números como representantes da harmonia do universo. Os irracionais não são inteiros (1, 2 etc.), frações (1/2, 2/3 etc.) ou números decimais, que seguem um padrão (no caso do número 0,22222..., por exemplo, o dois é repetido infinitamente). O número irracional é irregular, como a raiz quadrada de dois, que é igual a 1,414213562373...! O aluno Hipaso descobriu que esse era um número diferente dos que os gregos conheciam e contou ao mestre. Pitágoras o condenou à morte.
Segundo o filósofo, fenômenos físicos e naturais seguiam leis matemáticas. Ele provou sua idéia quando, em frente a uma oficina de ferreiro, o som de martelos golpeando o ferro chamou sua atenção. Notou que alguns martelos, usados ao mesmo tempo, produziam som gostoso de escutar. Mas quando determinado martelo unia-se ao coro... o ruído incomodava os ouvidos!
Pitágoras observou os martelos. A massa dos que geravam som agradável eram proporções (ou frações) da massa dos demais. Martelos com a metade ou dois terços da massa de outro martelo produziam som harmonioso quando usados juntos. A massa do martelo que criava ruído não tinha relação numérica com a massa dos outros. O mesmo acontecia com cordas do tetracórdio, um instrumento musical. Ao tocar uma corda do tetracórdio sem prendê-la, era criado um som. Ao prender a corda em pontos que correspondiam à metade, um terço ou um quarto de seu comprimento, o som tinha harmonia com o som gerado quando se toca a corda não presa.
Antes os cientistas formulavam hipóteses, comprovadas em alguns experimentos, que podiam ser negadas a qualquer momento, pois nada era universal. Quando Pitágoras provou que leis matemáticas governam fenômenos físicos, elas passaram a ser usadas para criar teorias científicas mais precisas.
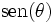como sendo a razão entre o cateto oposto a θ e a hipotenusa deste triângulo. Ou seja:
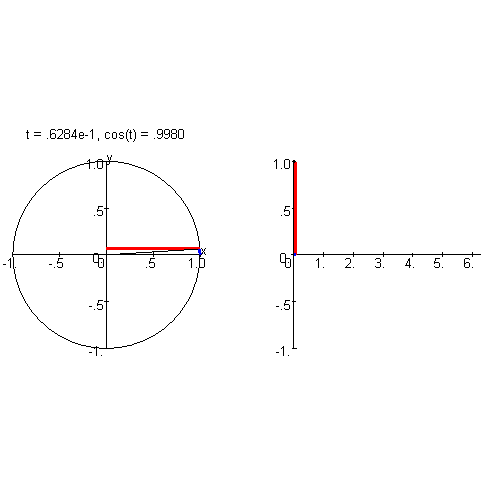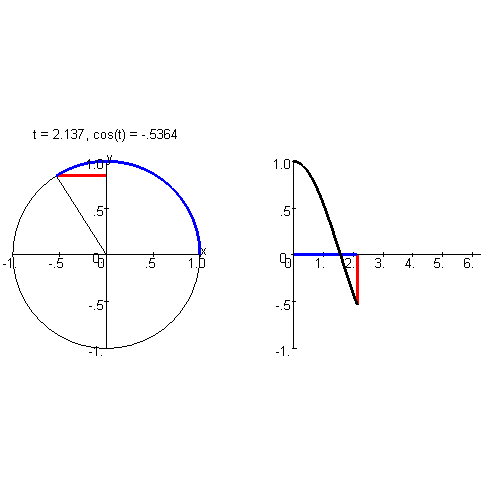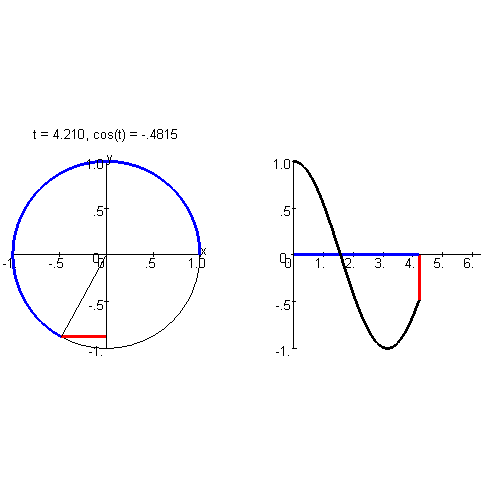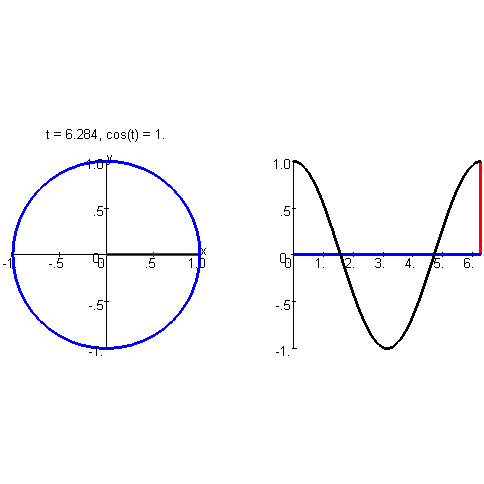
é igual ao co-seno de 
. Portanto:
