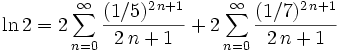Origem: Wikipédia, a enciclopédia livre.
Na Matemática, o logaritmo de base b, maior que zero e diferente de 1, é uma função de domínio  e imagem
e imagem  , bijetora e contínua que retorna o expoente na equação bn = x. Usualmente é escrito como logb x = n. Por exemplo: 34 = 81, portantolog381 = 4. Em termos simples o logaritmo é o expoente que uma dada base deve ter para produzir certa potência. No último exemplo o logaritmo de 81 na base 3 é 4, pois 4 é o expoente que a base 3 deve usar para resultar 81.
, bijetora e contínua que retorna o expoente na equação bn = x. Usualmente é escrito como logb x = n. Por exemplo: 34 = 81, portantolog381 = 4. Em termos simples o logaritmo é o expoente que uma dada base deve ter para produzir certa potência. No último exemplo o logaritmo de 81 na base 3 é 4, pois 4 é o expoente que a base 3 deve usar para resultar 81.
O logaritmo é uma de três funções intimamente relacionadas. Com bn = x, b pode ser determinado utilizando radicais, n com logaritmos, e x com exponenciais.
Um antilogaritmo é usado para mostrar o inverso de um logaritmo. Ele é escrito da seguinte maneira: antilogb(n) e significa o mesmo que bn.
Um logaritmo duplo é a inversa da exponencial dupla. Um super-logaritmo ou hiper-logaritmo é a inversa da função super-exponencial. O super-logaritmo de x cresce ainda mais lentamente que o logaritmo duplo para x grande.
Um logaritmo discreto é uma noção relacionada na teoria finita de grupos. Para alguns grupos finitos, acredita-se que logaritmo discreto seja muito difícil de ser calculado, enquanto exponenciais discretas são bem fáceis. Esta assimetria tem aplicações emcriptografia.
Logaritmos e exponenciais: inversas
Logaritmos em várias bases: vermelho representa a base
e, verde a base 10, e lilás a base 1,7. Note como logaritmos de todas as bases passam pelo ponto (1, 0).
Para cada base (b em bn), existe uma função logaritmo e uma função exponencial; elas são as funções inversas. Com bn = x:
- Exponenciais determinam x quando dado n; para encontrar x, se multiplica b por b (n) vezes.
- Logaritmos determinam n quando dado x; n é o número de vezes que x precisa ser dividido por b para se obter 1.
Para diferenciar o gráfico da função logarítmica do gráfico da função exponencial, pode-se utilizar a Regra da Mão Direita:
Como diferenciar os gráficos da funções log e exponencial a partir da mão direita.
Usando logaritmos
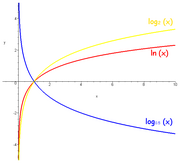
Três curvas para três bases diferentes: b = 2 (curva amarela), b = e (curva vermelha) e b = 0,5 (curva azul).
Uma função log
b(
x) é definida quando
x é um
número real positivo e
b é um número real positivo diferente de 1. Veja
identidades logarítmicas para várias leis que definem as funções logarítmicas. Logaritmos podem também ser definidos para argumentos
complexos. Isso é explicado na página do
logaritmo natural.
Para inteiros b e x, o número logb(x) é irracional (i.e., não é um quociente de dois inteiros) se b ou x possui um fator primo que o outro não possui (e em particular se eles são co-primos e ambos maiores que 1). Em alguns casos este fato pode ser provado rapidamente: por exemplo, se log23 fosse racional, ter-se-ia log23 = n/m para alguns inteiros positivos n e m, implicando que 2n = 3m. Mas essa última identidade é impossível, uma vez que 2n é par e 3m é ímpar.
Bases não especificadas
- Matemáticos geralmente entendem "ln(x)" como significando loge(x), i.e., o logaritmo neperiano de x, e escrevem simplesmente"log(x)" se o logaritmo na base-10 de x é procurado.
- Engenheiros, biólogos e outros escrevem apenas "ln(x)" ou (ocasionalmente) "loge(x)" quando se trata do logaritmo natural de x, e tomam "log(x)" para log10(x) ou, no contexto da computação, log2(x).
- Algumas vezes Log(x) (L maiúsculo) é usado significando log10(x), pelas pessoas que usam log(x) com l minúsculo significando loge(x).
- A notação Log(x) também é usada pelos matemáticos para se referir ao ramo principal da função logaritmo natural.
A maior parte das razões para se pensar em logaritmos na base 10 tornaram-se obsoletas logo após 1970 quando calculadoras de mão se tornaram populares (para mais sobre esse assunto, veja logaritmo comum). Não obstante, uma vez que calculadoras são feitas e normalmente usadas por engenheiros, as convenções usadas por eles foram incorporadas nas calculadoras, agora a maioria dos não-matemáticos tomam "log(x)" como o logaritmo na base 10 de x e usam "ln(x)" para se referir ao logaritmo natural dex. A notação "ln" foi introduzida em 1893 por Irving Stringham, professor de matemática da Universidade de Berkeley. Até 2005, alguns matemáticos adotaram a notação "ln", mas a maioria usa "log". Em Ciência da Computação o logaritmo na base 2 é escrito como lg(x) para evitar confusão. Este uso foi sugerido por Edward Reingold e popularizado por Donald Knuth.
Quando "log" é escrito sem uma base (b faltando em logb), o significado pode normalmente ser determinado através do contexto:
Mudança de base
Apesar de existirem identidades muito úteis, a mais importante para o uso na calculadora é a que permite encontrar logaritmos com bases que não as que foram programadas na calculadora (normalmente loge e log10). Para encontrar um logaritmo com uma base busando qualquer outra base a:

Prova da fórmula de mudança de base | por definição |
 | aplica-se  em ambos os lados em ambos os lados |
 | simplifica-se o lado esquerdo da igualdade |
 | divide-se por logk(b) |
Tudo isso implica que todas as funções logaritmo (qualquer que seja sua base) são similares umas às outras.
Usos dos logaritmos
Logaritmos são úteis para se resolver equações cujos expoentes são desconhecidos. Eles possuem derivadas simples, por isso eles são comumente usados como soluções de integrais. Além disso, várias quantidades na ciência são expressas como logaritmos de outras quantidades; veja escala logarítmica para uma explicação e uma lista.
Funções exponenciais
Algumas vezes (especialmente em análise) é necessário calcular funções exponenciais arbitrárias f(x)x usando se apenas aexponencial natural ex:
= exlog(f(x))
Cálculos mais fáceis
Logaritmos trocam números por expoentes. Mantendo-se a mesma base, é possível tornar algumas poucas operações mais fáceis:
| Operação com números | Operação com expoentes | Identidade logarítmica |
|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
Demonstração da identidade log(a) + log(b) = log(ab)
Por definição, se: log(a) = x então a = 10x. Logo, considerando-se b = 10y, tem-se:

Observa-se em ambos os lados da expressão acima que x + y = x + y, o que comprova a identidade.
Antes da calculadora eletrônica, isto fazia com que operações difíceis de dois números fossem muito mais fáceis. Simplesmente se achavam os logaritmos dos dois números (multiplique e divida) ou o primeiro número (potência ou raiz, onde um número já é um expoente) em uma tabela de logaritmos comuns, realizava-se uma operação mais simples neles, e se encontrava o resultado numa tabela. Réguas de cálculo realizavam as mesmas operações usando logaritmos, mas mais rapidamente e com menor precisão do que usando tabelas. Outras ferramentas para realizar multiplicações antes da invenção da calculadora incluem Napier's bones e calculadoras mecânicas.
Na álgebra abstrata, esta propriedade das funções logarítmicas pode ser resumida observando-se que qualquer uma delas com uma base fixa é um isomorfismo do grupo de números reais estritamente positivos sobre a multiplicação para o grupo de todos os números reais sobre a adição.
Cálculo
Para calcular a derivada de uma função logarítmica a seguinte fórmula é usada :  onde ln é o logaritmo natural, i.e. com a base e. Fazendo b = e:
onde ln é o logaritmo natural, i.e. com a base e. Fazendo b = e:

A seguinte fórmula é para obter a integral da função logaritmo

História
Joost Bürgi, um relojoeiro suíço a serviço do Duque de Hesse-Kassel, foi o primeiro a formar uma concepção sobre logaritmos. O método dos logaritmos naturais foi proposto pela primeira vez em 1614, em um livro intitulado Mirifici Logarithmorum Canonis De ioescrito por John Napier, Barão de Merchiston na Escócia, quatro anos após a publicação de sua memorável invenção. Este método contribuiu para o avanço da ciência, e especialmente a astronomia, fazendo com que cálculos muito difíceis se tornassem possíveis. Anterior à invenção de calculadoras e computadores, era uma ferramenta constantemente usada em observações, navegação e outros ramos da matemática prática. Além de sua imensa utilidade na realização de cálculos práticos, os logaritmos também têm um papel muito importante em matemática teórica.
De início, Napier chamou os logaritmos de "números artificiais" e os antilogaritmos de "números naturais". Mais tarde, Napier formou a palavra logaritmo, para significar um número que indica uma razão: λoγoς (logos) que significa razão, e αριθμoς (arithmos) significando número. Napier escolheu dessa forma porque a diferença entre dois logaritmos determina a razão entre os números dos quais eles são tomados, de forma que uma série aritmética de logaritmos corresponde a uma série geométrica de números. O termo antilogaritmo foi introduzido no final do século XVII e, apesar de nunca ter sido usado muito na matemática, persistiu em coleções de tabelas até não ser mais usado.
Napier não usou uma base como a concebemos hoje, mas seus logaritmos eram na base  . Para facilitar interpolações e cálculos, é útil fazer a razão r na série geométrica próximo de 1. Napier escolheu r = 1 − 10 − 7 = 0,999999, e Bürgi escolheu r = 1 + 10 − 4 = 1,0001. Os logaritmos originais de Napier não tinham log 1=0, ao invés disso tinham log 107 = 0. Desse modo se N é um número e Lé seu logaritmo tal qual calculado por Napier, N = 107(1 − 10 − 7)L. Uma vez que (1 − 10 − 7) é aproximadamente 1 / e, L é aproximadamente 107log1 / eN / 107.
. Para facilitar interpolações e cálculos, é útil fazer a razão r na série geométrica próximo de 1. Napier escolheu r = 1 − 10 − 7 = 0,999999, e Bürgi escolheu r = 1 + 10 − 4 = 1,0001. Os logaritmos originais de Napier não tinham log 1=0, ao invés disso tinham log 107 = 0. Desse modo se N é um número e Lé seu logaritmo tal qual calculado por Napier, N = 107(1 − 10 − 7)L. Uma vez que (1 − 10 − 7) é aproximadamente 1 / e, L é aproximadamente 107log1 / eN / 107.
Tabelas de logaritmos
Antes do advento do computador e da calculadora, usar logaritmos significava usar tabelas de logaritmos, que tinham de ser criadas manualmente. Logaritmos de base-10 são úteis em cálculos quando meios eletrônicos não são disponíveis. Veja logaritmo comum para detalhes, incluindo o uso de características e mantissas de logaritmos comuns (i.e., base-10).
Em 1617, Briggs publicou a primeira versão de sua própria lista de logaritmos comuns, contendo os logaritmos com 8 dígitos de todos os inteiros inferiores a 1.000. Em 1624 ele publicou ainda outra, "Aritmética Logaritima", contendo os logaritmos de todos os inteiros de 1 a 20.000 e de 90.000 a 100.000, juntos com uma introdução que explicava a história, a teoria e o uso dos logaritmos. O intervalo de 20.000 a 90.000 foi preenchido por Adrian Vlacq; mas em sua tabela, que apareceu em 1628, os logaritmos eram de somente 10 dígitos.
Foram descobertos mais tarde 603 erros na tabela de Vlacq, mas "isso não pode ser considerado uma grande quantidade, quando se é considerado que a tabela foi um resultado de um cálculo original, e que é possível haver erros quando mais de 2.100.000 números são utilizados." (Athenaeum, 15 de Junho de 1872. Veja também as "Notícias Mensais da Sociedade Real de Astronomia" de Maio, 1872.) Uma edição do trabalho de Vlacq, contendo diversas correções, foi publicado em Leipzig, 1794, titulado de "Thesaurus Logarithmorum Completus" por Jurij Vegal.
A tabela de 7 dígitos de Callet (Paris, 1795), ao invés de parar em 100.000, dava os logaritmos de oito dígitos dos números entre 100.000 e 108.000, visando diminuir os erros de interpolação, que eram grandes no início da tabela; e essa adição era geralmente incluída em tabelas de 7 dígitos. A única extensão publicada importante da tabela de Vlacq foi feita por Mr. Sang, em 1871, cuja tabela tinha os logaritmos de 7 casas de todos os números abaixo de 200.000.
Briggs e Vlacq também publicaram tabelas originais de logaritmos de funções trigonométricas.
Além das tabelas mencionadas acima, uma grande coleção, chamada Tables du Cadastre, foi feita sob a direção de Prony, por um cálculo original, sob a ajuda do governo republicano francês. Esse trabalho, que continha os logaritmos de 9 dígitos de todos os números até o 100.000, e de 24 dígitos dos números entre 100.000 e 200.000, existe apenas no manuscrito in seventeen enormous folios, no observatório de Paris. Esse trabalho foi iniciado em 1792, e para garantir uma grande precisão de todos os cálculos, o trabalho foi realizado de duas formas diferentes, e ambos os manuscritos foram subsequentemente e cuidadosamente unidos, tendo todo o trabalho sido realizado em um período de dois anos (English Cyclopaedia, Biography, Vol. IV., artigo "Prony"). Interpolação cúbica poderia ser utilizada para encontrar o valor dos logaritmos, com uma precisão similar.
Para os estudantes de hoje, que contam com a ajuda de calculadoras, o trabalho a respeito das tabelas acima mencionada, é pequeno para o avanço dos logaritmos.
Algoritmo
Para calcular logb(x) se b e x são números racionais e x ≥ b > 1:
Se n0 é o maior número natural tal que bn0 ≤ x ou, alternativamente,

então

Este algoritmo recursivamente produz a fração contínua

Para usar um número irracional como entrada, basta aplicar o algoritmo a sucessivas aproximações racionais. O limite daSucessão_matemática resultante deve convergir para o resultado correto.
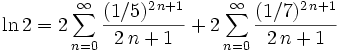
Trivia
Notação alternativa
Algumas pessoas usam a notação blog(x) em vez de logb(x).
Relações entre logaritmos comum, natural e binário
Em particular, temos os seguintes resultados:
- log2(e) ≈ 1,44269504
- log2(10) ≈ 3,32192809
- loge(10) ≈ 2,30258509
- loge(2) ≈ 0,693147181
- log10(2) ≈ 0,301029996
- log10(e) ≈ 0,434294482
Um relação curiosa é a aproximação log2(x) ≈ log10(x) + ln(x), com precisão de 99,4%, ou 2 dígitos significativos. Isso porque1/ln(2) − 1/ln(10) ≈ 1 (na verdade vale 1,0084...).
Outra relação interessante é a aproximação log10(2) ≈ 0,3 (na verdade vale 0,301029995). Com isso, com um erro de apenas de 2,4%, 210 ≈ 103,ou seja, 1024 é aproximadamente 1000.
 e imagem
e imagem  , bijetora e contínua que retorna o
, bijetora e contínua que retorna o 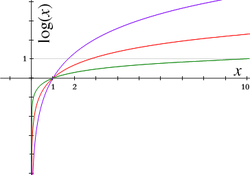




 em ambos os lados
em ambos os lados















 onde ln é o logaritmo natural, i.e. com a base e. Fazendo b = e:
onde ln é o logaritmo natural, i.e. com a base e. Fazendo b = e:

 . Para facilitar interpolações e cálculos, é útil fazer a razão
. Para facilitar interpolações e cálculos, é útil fazer a razão