Conjuntos: Igualdade

Igualdades

Tudo bem pessoal? No último artigo sobre Conjuntos, vimos que um conjunto pode ser uma coleção de qualquer objeto, e também aprendemos como determinar este conjunto.

Hoje vamos dar mais um passo na direção deste imenso mundo abstrato.

Igualdades de conjuntos

Dois conjuntos são iguais quando possuem os mesmos elementos. Por exemplo, se:
A = { Conjunto dos números naturais pares maiores do que 5 }
B = { 0, 2, 4, 6, 8, 10, 12,...}
C = { 6, 8, 10, 12,...}

Observe que temos três conjuntos, e somente dois deles são iguais. Você sabe diferenciar qual deles não é igual aos outros dois?

Veja o que o conjunto A esta pedindo.

“ Eu quero que você me diga, qual é o { conjunto dos números naturais pares maiores do que 5}”.Então vamos dizer para ele, que o conjunto dos números naturais maiores do que 5 é:

{ 6,8,10,12,...}, logo temos que C=A.

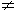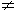Por que o conjunto B é do conjunto A? Veja que a condição é o conjunto seja maior do que 5. Como o conjunto B tem elementos menores do que 5 {0,2,4}, ele é diferente do conjunto A. Viu como é fácil!

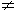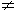Se A é igual a B, então escrevemos A = B, agora se A é diferente de B, escrevemos A B.

Mais exemplos:

a) O conjunto M={ 1,2} e o conjunto N={ 1, 1, 1, 1, 2, 2, 2, 2, 2, 2,2}. Observe que os dois conjuntos possuem penas dois elementos cada um, e exatamente iguais.

A quantidade de vezes que o elemento aparece no conjunto não é levada em consideração. Então temos que, M=N.

b) A = { x / x² = 9 } e B = { x / (x – 3)(x + 3) =0 }

Resolvendo a equação de cada conjunto obtemos em ambos os casos que x é igual a 3 ou -3 : A = {-3;3} e B = {-3;3} ,então temos que A=B, pois os elementos são exatamente iguais.

Simbolicamente teríamos A=B <=> (A C B) 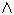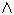(B C A)

Por hoje ficamos por aqui. No próximo artigo vamos começar a trabalhar com os conjuntos, vazio, unitário e universo. Se você quer baixar este conteúdo para imprimir acesse o seguinte arquivo: Igualdade de Conjuntos.

Veja também os Exercícios propostos